斜率优化dp

发表于 更新于

前言

经典题：P3195 [HNOI2008]玩具装箱
斜率优化题单
之前我们学习了单调队列优化 dp，它可以用来解决转移方程中有 $i,j$ 相关项的和。但是如果转移方程中有 $i,j$ 的乘积项 $f[i]=\min(f[j]+x \times a[i]+y \times a[j]+z \times a[i] \times a[j])(1\leqslant j < i)$，单调队列就无法解决这种问题了，因为对于不同的 $i$，$j$ 相关项的最小值并不相同。所以我们需要用新的方法来解决。

基本思路

我们再来改写一下转移方程，就变成：$f[j]+y \times a[j]=-z \times a[i] \times a[j]+f[i]-x \times a[i](1\leqslant j < i)$，当 $i$ 不变时，以 $j$ 为自变量，于是这个转移方程就变成了一个一次函数 $Y=A \times X+B$，其中 $Y=f[j]+y \times a[j]$，$A=-z \times a[i]$，$X=a[j]$，$B=f[i]-x \times a[i]$。如果我们要求 $f[i]$ 最小值，我们就是要求 $B$ 的最大值。我们先把已经求出的所有点 $P(X,Y)$ 画出来：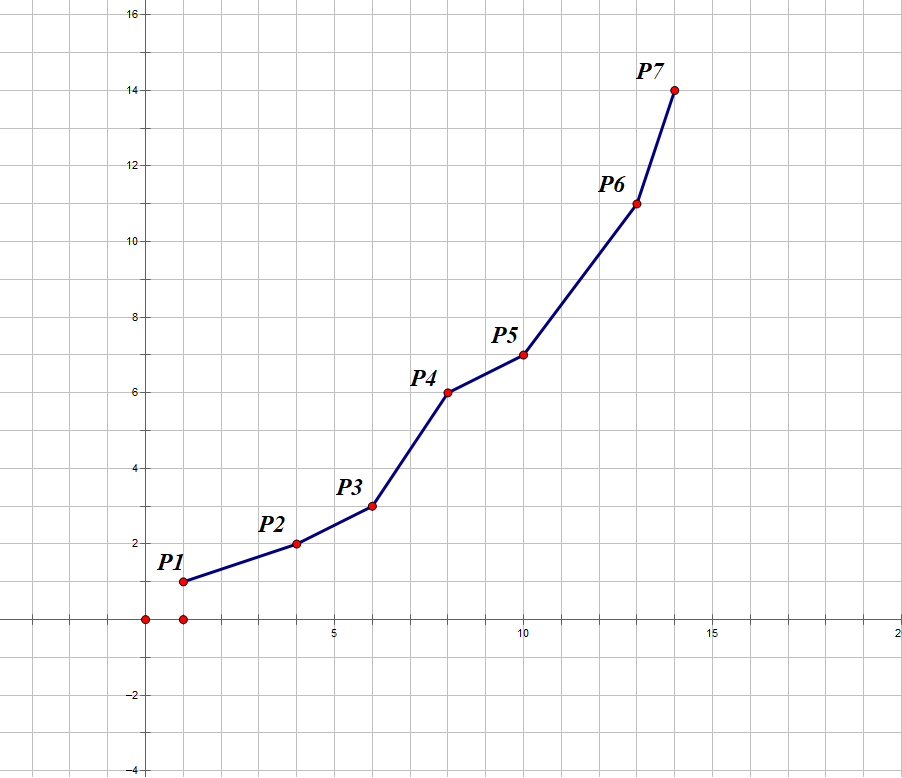
1
我们再画一条直线，直线的斜率就是 $A$，如果这条直线过点 $P(X_j,Y_j)$ ，那么对于这条直线这条直线就可以列出 $Y_j=A \times X_j+B$，而 $B$ 就是我们要求的值。我们就要让 $B$ 尽量地小，也就是直线要尽量靠下。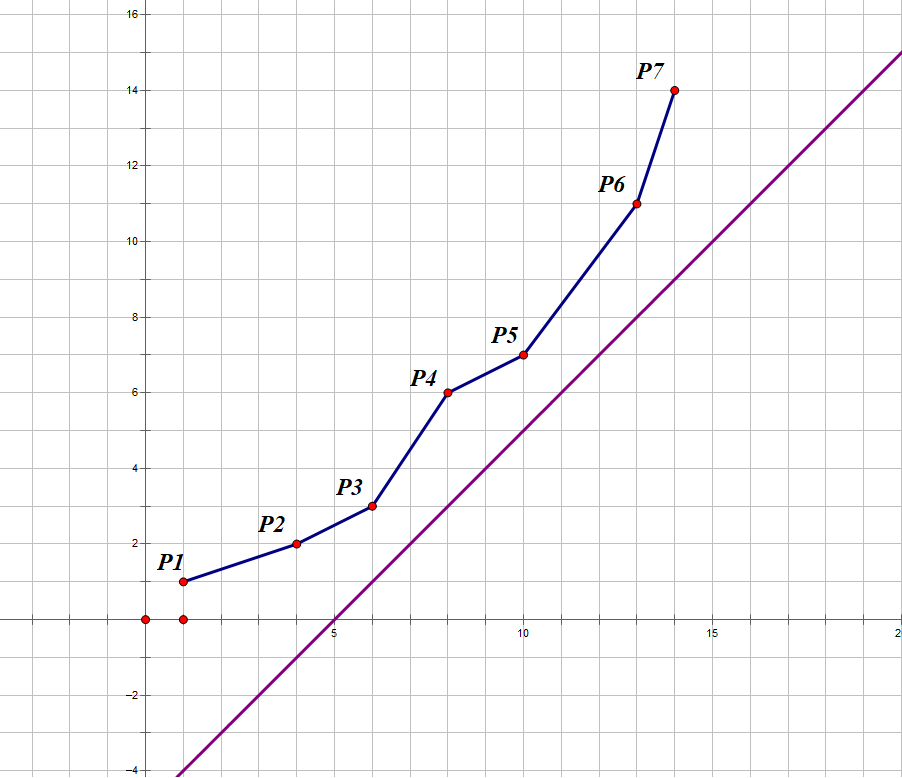
2
3

实现方法

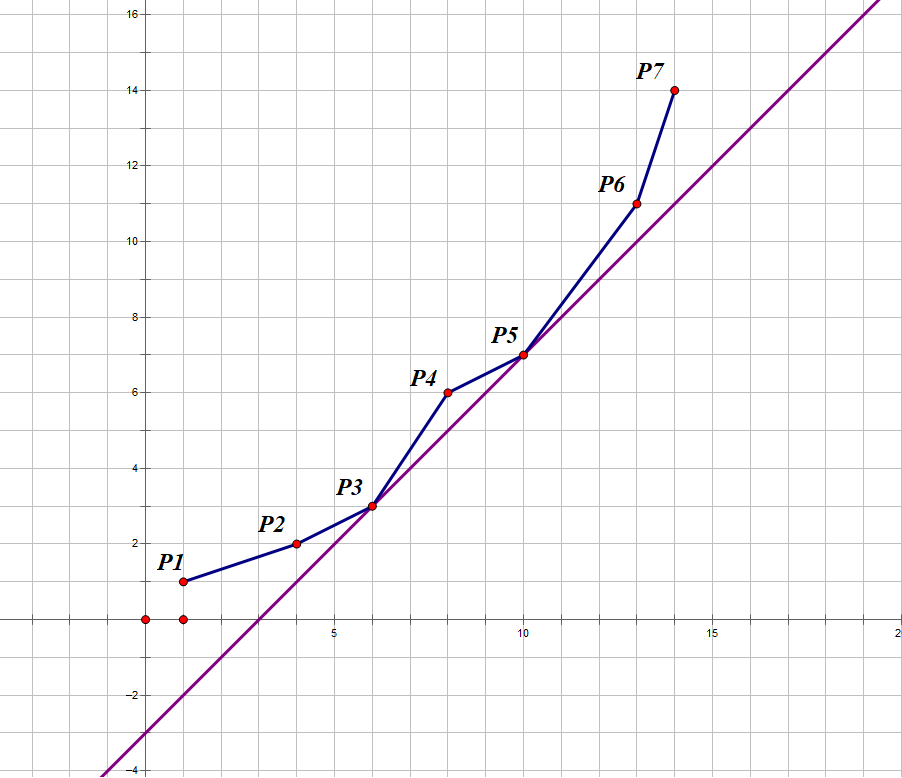
就像这样我们就找到了 $B$ 的最小值，那么我们要如何实现呢？我们可以发现，如果一个点与他左右的两个点形成了“上凸”的形状，如上图的 $P_4$，可以肯定，这个点不可能成为一个最优解，也就是任意斜率的直线在 $B$ 最小的时候都不会经过这个点，那么我们就可以删去这个点。于是图就变成了这样：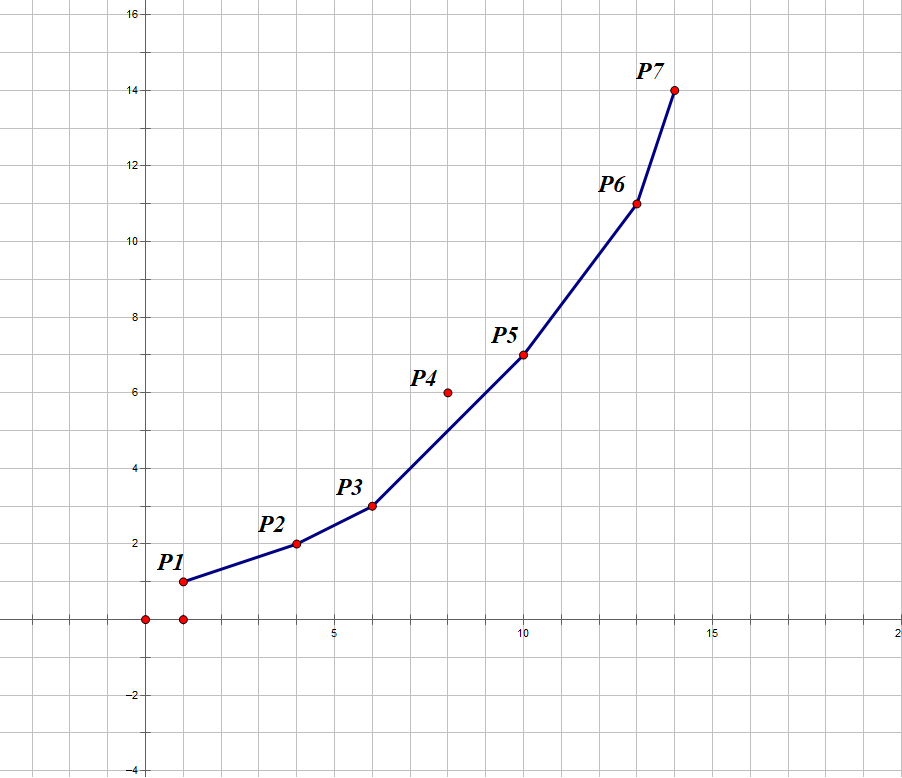
4
下图是三根不同斜率的直线在 $B$ 取得最小值的情况，可以发现，每一条线过的第一个点，左边的线段的斜率小于这条直线的斜率，右边的线段大于等于这条直线时，$B$ 取得最小值。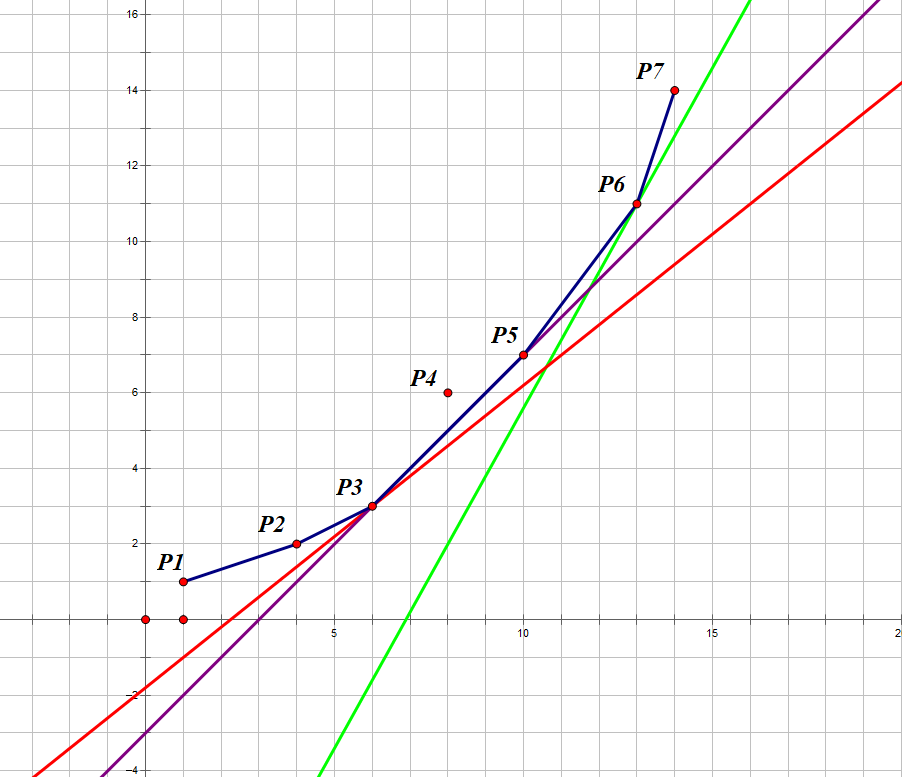
5
于是我们自然而然地想到二分查找，可以在 $O(n\log n)$ 的时间内完成。但是一般情况下，$a$ 是递增的，也就是说直线的斜率也是递增的。在这种情况下，我们又可以用单调队列了，只需要维护所有比当前直线斜率大的线段即可。枚举 $i$，对于每个 $i$：首先弹出队首，知道队首点和它的下一个点的线段斜率比直线 $i$ 的斜率小，就一直弹出队首。然后用队首点计算 $f[i]$。然后弹出队尾，如果队尾点与它的上一个点的线段斜率比点 $i(X_i,Y_i)$ 与队尾点的线段斜率大，也就是出现“上凸”，就一直弹出队尾。最后将点 $i$ 入队。
于是我们用 $O(n)$ 的时间完成了这个 dp，这就是著名的斜率优化。

总结

我们来总结一下斜率优化的普遍规律。对于一个转移方程，$Y$ 就是只与 $j$ 有关的项，$A$ 就是 $i,j$ 的乘积项中与 $i$ 有关的因式，$X$ 就是 $i,j$ 乘积项中与 $j$ 有关的因式，$B$ 就是只与 $i$ 有关的项。知道了这些，就可以轻松解决许多斜率优化 dp 的题目了。

注意事项

实现斜率优化时需要注意几点：注意最小值与最大值的区别，最大值的判断方法与最小值相反，也就是整个图形是上凸的，每一个直线 $B$ 最大的时候前一个线段斜率比它大，后一个线段斜率比它小。注意计算斜率时判断两个点横坐标是否相同，如果忽略则会导致出现 $\div 0$ 的情况出现，直接 $\color{purple}{\text{RE}}$。
但是有的时候数组 $a$ 并不单调，意味着直线的斜率也不是单调的，这是我们就需要保存所有的节点，每一次二分查找，时间 $O(n\log n)$。

code

此代码为经典题 P3195 的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1000001;
int n,m,a[N],Q[N*2],T=0,R=0;
ll b[N],c[N],f[N];
ll abc(int x,int y)
{
    if(c[x]==c[y]) return 1e18;
    return ((f[x]+c[x]*c[x])-(f[y]+c[y]*c[y]))/(c[x]-c[y]);
}
int main()
{
    scanf("%d%d",&n,&m);
    c[0]=m+1;
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);
        b[i]=b[i-1]+a[i]+1;
        c[i]=c[i-1]+a[i]+1;
    }
    for(int i=1;i<=n;++i)
    {
        while(T<R&&abc(Q[T],Q[T+1])<2*b[i]) ++T;
        f[i]=f[Q[T]]+b[i]*b[i]-2*b[i]*c[Q[T]]+c[Q[T]]*c[Q[T]];
        while(T<R&&abc(Q[R],i)<abc(Q[R-1],Q[R])) --R;
        Q[++R]=i;
    }
    printf("%lld",f[n]);
    return 0;
}
相关文章