平衡树Treap

发表于 更新于

前言

模板题：P3369 【模板】普通平衡树
在一堆元素中查找一个元素，线性查找需要 $O(n)$ 的时间，于是人们就发明了 BST 二叉搜索树，一个节点左子树上的元素的值总小于此节点的值，此节点的右子树上的元素的值总小于此节点的值。这样根据一个元素的值就可以快速（$O(\log n)$）在 BST 上查找到一个元素。BST 有一个特点，就是它的中序遍历序列就是所有元素排序后的结果。不过同样的一些元素组成的 BST 两个 BST 记录的是同一组数。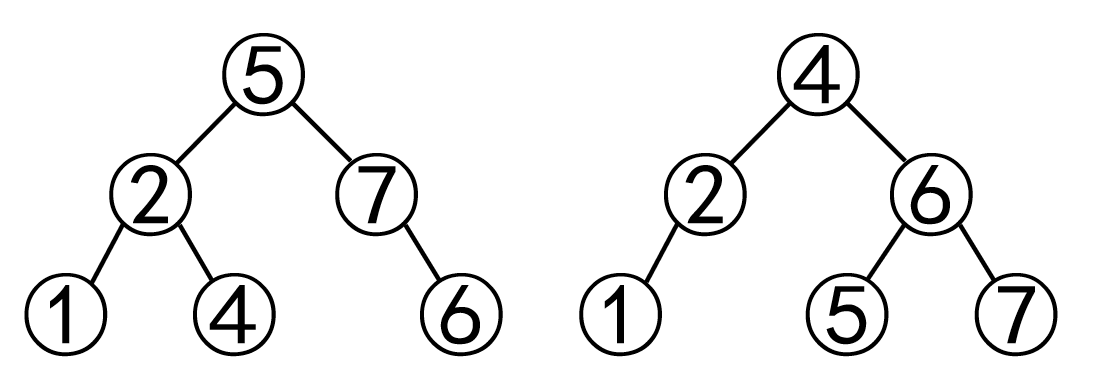
1
不过这样还是容易被卡，比如所有元素按照大小顺序加入 BST，这个 BST 就会退化为一个链，复杂度就退化为 $O(n)$ 了，如下图。
2
这时候我们就需要适当调整这个 BST 的形状，让这个 BST 更加平衡，于是又出现了平衡树，这里介绍一种较简单的平衡树，它就是 Treap。

基本思路

Treap 其实是一个合成词“Tree+Heap”，翻译过来就是树堆，它既有 BST 的性质，也有堆的性质。Treap 会在插入元素的时候给每个元素一个随机的优先级，然后通过旋转操作，使得它满足 BST 的同时，还要满足一个节点的优先级小于它的所有儿子的优先级。由于优先级是随机的，所以这个 BST 的形状是随机的，就不会出现被卡成一条链的情况（只要人品正常）。

储存及更新

1
2
3
4
struct treap
{
    int x,l,r,s,k,t;
}T[1000001];

平衡树的储存如上。Treap 的每个节点总共需要储存这几个值：这个节点的元素的值 $x$，这个节点的左、右儿子 $l,r$，这个节点的子树上总共的元素个数 $s$，这个节点的优先级 $k$ 和这个节点的元素个数 $t$。
平衡树需要动态更新当前子树的节点个数，我们就需要一个类似线段树的 pushup 函数，代码如下：

1
2
3
4
void pushup(int x)
{
    T[x].s=T[T[x].l].s+T[T[x].r].s+T[x].t;
}

旋转操作

Treap中非常难懂的一部分就是它的旋转操作，它可以改变 BST 的形状。旋转分为左旋与右旋。右旋操作其实就是将这个节点的父节点变为这个点的右子节点，这个点调整到原父节点的位置，并将这个点的右节点调整为其原父节点的左节点。如下图，从左图到右图的操作就是将 $2$ 号节点进行右旋。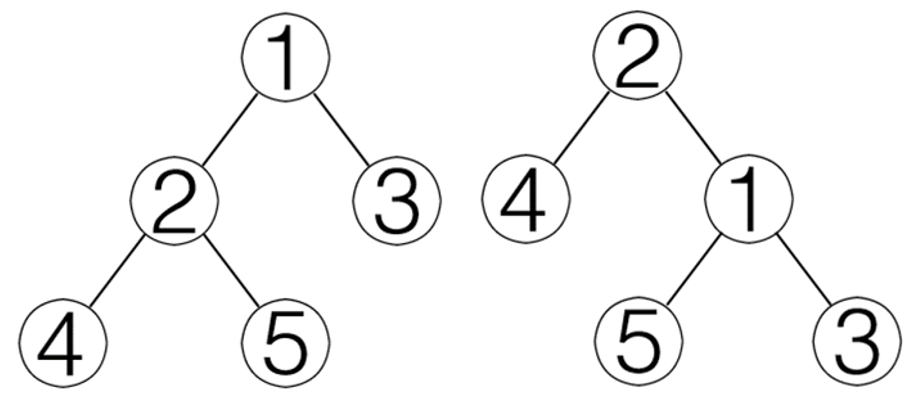
3
左旋的操作刚好和右旋相反。我们可以发现，第一个BST的中序遍历为 $4,2,5,1,3$ ，而第二个 $4,2,5,1,3$，这两个 BST 实质上记录的东西实质上是一样的，但是它的形状已经改变了。我们就可以通过旋转操作改变一个 BST 的形状。
由于旋转操作要改变指向当前节点的指针，所以我们要使用传址的方法，这样在旋转改变当前节点的时候在调用它的函数中的指针也会改变。
旋转操作的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void rotate_l(int &x)
{
    int p=T[x].r;
    T[x].r=T[p].l;
    T[p].l=x;
    T[p].s=T[x].s;
    x=p;
    pushup(x);
    pushup(T[x].l);
}
void rotate_r(int &x)
{
    int p=T[x].l;
    T[x].l=T[p].r;
    T[p].r=x;
    T[p].s=T[x].s;
    x=p;
    pushup(x);
    pushup(T[x].r);
}

插入操作

Treap 的插入操作很简单，只需要一直找到对应元素值与插入值相等的位置或者发现不存在值相等的元素即可。如果我们要插入的元素值为 $k$，每到一个节点，如果对应元素值等于 $k$，就把这个点的元素个数加一；如果 $k$ 小于这个点的元素值，那么就进入这个点的左子节点；如果 $k$ 大于这个点的元素值，那么就进入这个点的右子节点；如果这个点的编号为 $0$，那么表明不存在与 $k$ 相等的元素，就新建一个节点，并随机赋优先级。
插入操作看似很简单，但是这样有可能不满足堆的性质，我们就需要进行旋转操作。如果左节点的优先级比这个节点小，那么就将这个节点右旋；如果右子节点的优先级比这个节点小，那么就将这个节点左旋。并且更新 Treap 的状态。
同样，插入操作由于要旋转，也要通过传址的方法传参。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void add(int &x,int k)
{
    if(x==0)
    {
        x=++q;
        T[x].l=T[x].r=0;
        T[x].s=T[x].t=1;
        T[x].k=k;
        T[x].h=rand()*rand()%1000000+1;
        return;
    }
    if(k==T[x].k) ++T[x].t;
    else if(k<T[x].k) add(T[x].l,k);
    else if(k>T[x].k) add(T[x].r,k);
    if(T[x].l!=0&&T[x].h>T[T[x].l].h) rotate_r(x);
    if(T[x].r!=0&&T[x].h>T[T[x].r].h) rotate_l(x);
    pushup(x);
}

删除操作

Treap 的删除操作和插入操作相似，要一直找到对应元素值与删除值相等的位置，然后把这个位置的元素个数减一，如果个数为 $0$ 了，就删除这个节点，并将优先级较小的子节点放在这个位置，不过这时需要注意左右子节点是否存在。如果不存在这个节点，就说明没有这个元素。同样，最后的时候要更新结点个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void remove(int &x,int k)
{
    if(x==0) return;
    if(k==T[x].k)
    {
        if(T[x].t>1)
        {
        	--T[x].t;
            pushup(x);
            return;
        }
        if(T[x].l==0&&T[x].r==0)
        {
            x=0;
            return;
        }
        if(T[x].l!=0&&(T[x].r==0||T[T[x].l].h<T[T[x].r].h))
        {
            rotate_r(x);
            remove(T[x].r,k);
        }
        else
        {   
            rotate_l(x);
            remove(T[x].l,k);
        }
        pushup(x);
        return;
    }
    if(k<T[x].k) remove(T[x].l,k);
    else remove(T[x].r,k);
    pushup(x);
}

查询排名

在 Treap 中查询一个元素的排名，只需要像之前一样一直访问直到找到这个元素即可。根节点在当前子树的排名就是左子树的大小加一，而左子树的所有节点的排名就是这个节点在左子树中的排名，右子树的所有节点的排名就是这个节点在右子树的排名加上左子树以及根节点的大小。由于访问不需要修改节点，就不需要再传址了。

1
2
3
4
5
6
7
int num(int x,int k)
{
    if(x==0) return 1;
    if(k==T[x].k) return T[T[x].l].s+1;
    if(k<T[x].k) return num(T[x].l,k);
    return T[T[x].l].s+T[x].t+num(T[x].r,k);
}

查询对应排名的元素

要查询相应排名的元素，只需要在每一次判断这个元素在当前节点的根节点、左子树还是右子树上。如果当前子树中的排名小于左子树的大小，那么这个元素就在左子树中，这个元素在左子树中的排名就是当前子树中的排名；如果不在左子树中但是排名小于等于左子树大小加上根节点的大小，那么这个元素就是根节点的元素值；否则就在右子树中，在右子树中的排名就是在当前子树中的排名减去左子树的大小和根节点的大小。

1
2
3
4
5
6
7
int sum(int x,int k)
{
    if(x==0) return 1e9;
    if(k<T[T[x].l].s+1) return sum(T[x].l,k);
    if(k<=T[T[x].l].s+T[x].t) return T[x].k;
    return sum(T[x].r,k-T[T[x].l].s-T[x].t);
}

查询前驱和后继

一个点的前驱指的是小于这个元素值的最大的元素，后继指的是大于这个元素值的最小的元素。要找到一个点的前驱，当这个点在这个子树中时，如果要找的元素值小于等于根节点的元素值，说明这个元素在左子树中，就搜索左子树，否则在右子树中或者就是根节点，就搜索右子树。如果在左子树中但是最后没有找到，也就是返回了 $0$，说明这个节点没有在这个子树中，返回 $0$。如果在右子树中没有找到，说明这个元素的前驱就是根节点。最后，返回找到的元素或者 $0$。后继的查询操作刚好相反。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int find_f(int x,int k)
{
    if(x==0) return 0;
    if(k<=T[x].k) return find_f(T[x].l,k);
    int p=find_f(T[x].r,k);
    if(p==0) return T[x].k;
    return p;
}
int find_b(int x,int k)
{
    if(x==0) return 0;
    if(k>=T[x].k) return find_b(T[x].r,k);
    int p=find_b(T[x].l,k);
    if(p==0) return T[x].k;
    return p;
}

Treap函数的调用

我们总共学习了 $6$ 个 Treap 的相关函数。调用的时候我们需要调用 Treap 的根节点。由于 Treap 的形状在时刻变化，所以我们需要用一个变量 $r$ 来记录根节点，初始值为 $0$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main()
{
    srand(time(NULL));
    scanf("%d",&m);
    for(int i=1;i<=m;++i)
    {
        int z,k;
        scanf("%d%d",&z,&k);
        if(z==1) add(r,k);
        else if(z==2) remove(r,k);
        else if(z==3) printf("%d\n",num(r,k));
        else if(z==4) printf("%d\n",sum(r,k));
        else if(z==5) printf("%d\n",find_f(r,k));
        else if(z==6) printf("%d\n",find_b(r,k));
    }
    return 0;
}

code

#include<cstdio>
#include<algorithm>
#include<ctime>
using namespace std;
int m,r=0,q=0;
struct treap
{
    int k,l,r,s,h,t;
}T[1000001];
void pushup(int x)
{
    T[x].s=T[T[x].l].s+T[T[x].r].s+T[x].t;
}
void rotate_l(int &x)
{
    int p=T[x].r;
    T[x].r=T[p].l;
    T[p].l=x;
    T[p].s=T[x].s;
    x=p;
    pushup(x);
    pushup(T[x].l);
}
void rotate_r(int &x)
{
    int p=T[x].l;
    T[x].l=T[p].r;
    T[p].r=x;
    T[p].s=T[x].s;
    x=p;
    pushup(x);
    pushup(T[x].r);
}
void add(int &x,int k)
{
    if(x==0)
    {
        x=++q;
        T[x].l=T[x].r=0;
        T[x].s=T[x].t=1;
        T[x].k=k;
        T[x].h=rand()*rand()%1000000+1;
        return;
    }
    if(k==T[x].k) ++T[x].t;
    else if(k<T[x].k) add(T[x].l,k);
    else if(k>T[x].k) add(T[x].r,k);
    if(T[x].l!=0&&T[x].h>T[T[x].l].h) rotate_r(x);
    if(T[x].r!=0&&T[x].h>T[T[x].r].h) rotate_l(x);
    pushup(x);
}
void remove(int &x,int k)
{
    if(x==0) return;
    if(k==T[x].k)
    {
        if(T[x].t>1)
        {
            --T[x].t;
            pushup(x);
            return;
        }
        if(T[x].l==0&&T[x].r==0)
        {
            x=0;
            return;
        }
        if(T[x].l!=0&&(T[x].r==0||T[T[x].l].h<T[T[x].r].h))
        {
            rotate_r(x);
            remove(T[x].r,k);
        }
        else
        {   
            rotate_l(x);
            remove(T[x].l,k);
        }
        pushup(x);
        return;
    }
    if(k<T[x].k) remove(T[x].l,k);
    else remove(T[x].r,k);
    pushup(x);
}
int num(int x,int k)
{
    if(x==0) return 1;
    if(k==T[x].k) return T[T[x].l].s+1;
    if(k<T[x].k) return num(T[x].l,k);
    return T[T[x].l].s+T[x].t+num(T[x].r,k);
}
int sum(int x,int k)
{
    if(x==0) return 1e9;
    if(k<T[T[x].l].s+1) return sum(T[x].l,k);
    if(k<=T[T[x].l].s+T[x].t) return T[x].k;
    return sum(T[x].r,k-T[T[x].l].s-T[x].t);
}
int find_f(int x,int k)
{
    if(x==0) return 0;
    if(k<=T[x].k) return find_f(T[x].l,k);
    int p=find_f(T[x].r,k);
    if(p==0) return T[x].k;
    return p;
}
int find_b(int x,int k)
{
    if(x==0) return 0;
    if(k>=T[x].k) return find_b(T[x].r,k);
    int p=find_b(T[x].l,k);
    if(p==0) return T[x].k;
    return p;
}
int main()
{
    srand(time(NULL));
    scanf("%d",&m);
    for(int i=1;i<=m;++i)
    {
        int z,k;
        scanf("%d%d",&z,&k);
        if(z==1) add(r,k);
        else if(z==2) remove(r,k);
        else if(z==3) printf("%d\n",num(r,k));
        else if(z==4) printf("%d\n",sum(r,k));
        else if(z==5) printf("%d\n",find_f(r,k));
        else if(z==6) printf("%d\n",find_b(r,k));
    }
    return 0;
}
相关文章